

|
|
 |
|

La découverte de la petitesse de la Terre a été faite, comme tant d'autres découvertes importantes, au Moyen-Orient, au 111e siècle avant Jésus-Christ (276 -194 av JC), dans la plus grande métropole de l'époque: Alexandrie, en Égypte. Là vivait un homme du nom d'Êratosthène. Un de ses contemporains jaloux le surnomma «Bêta», de la seconde lettre de l'alphabet grec, car, disait-il, Eratosthène était en tout le second. Mais il semble évident qu'Eratosthène méritait plutôt le surnom d' «Alpha». Astronome, historien, géographe, philosophe, poète, critique de théâtre et mathématicien, son oeuvre comprend des titres variés, comme l'Astronomie et Se libérer de la Douleur. Il dirigeait la grande bibliothèque d'Alexandrie, et c'est là qu'un jour un papyrus attira son attention sur un nouveau sujet. Il y lut qu'à Syène, ville frontière du Sud située près des premières chutes du Nil, le 21 juin à midi, un bâton planté à la verticale ne jetait pas d'ombre. Au solstice d'été, le jour le plus long de l'année, alors que midi approchait, les ombres des colonnes du temple raccourcissaient. A midi, elles avaient disparu. Et on pouvait voir le Soleil se refléter au fond d'un puits profond, qu'il surplombait très exactement. Tout autre que lui aurait négligé cette observation. Des bâtons verticaux, des ombres, un reflet au fond d'un puits, la position du Soleil, quelle importance pouvaient bien avoir des choses aussi simples et quotidiennes? Mais Eratosthène était un esprit scientifique, et en réfléchissant sur ces apparentes banalités, il changea le monde; on pourrait presque dire qu'il refit le monde.

Vue prise du fond du puits de l'ancienne Syène, ville située autrefois à côté de l'actuelle Abu Simbel, en Egypte.
Eratosthène y aurait entreprit son étude de la circonférence de la terre.
Car il eut la présence d'esprit de vérifier Si, autour de midi, le 21juin, à Alexandrie, un bâton vertical jetait une ombre. L'expérience fut positive. Il se posa alors la question suivante: comment se fait-il qu'à Syène un bâton planté verticalement n'ait pas d'ombre, alors qu'au même moment, mais beaucoup plus au nord, à Alexandrie, il se produit l'effet contraire? Prenons une carte de l'Egypte ancienne et deux épingles. Plantons-en une sur Alexandrie et l'autre sur Syène. Supposons qu'à un moment donné aucune de ces deux épingles ne projette d'ombre. Il n'y a là rien d'étonnant - puisqu'il s'agit d'une surface plane. La lumière l'éclaire directement. Le fait que les deux épingles projettent des ombres de longueurs identiques serait tout aussi normal, sur une surface plane: les rayons lumineux formeraient avec les deux épingles un angle de mesure égale. Mais comment faire pour qu'au même moment l'épingle plantée sur Syène n'ait pas d'ombre et que celle d'Alexandrie en projette une très nette?
|
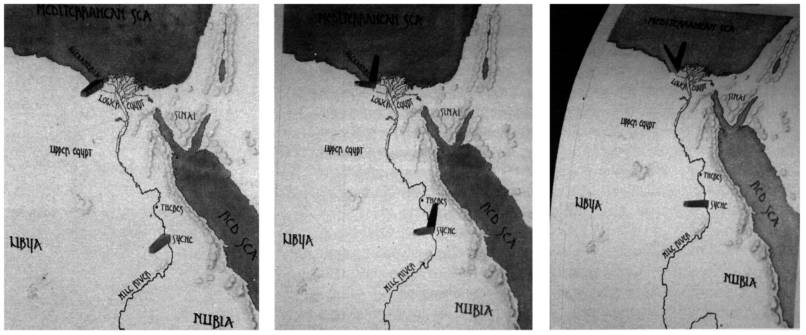
Carte plane de l'Egypte ancienne. Le soleil à la verticale, les obélisques d'Alexandrie et de Syène n'ont pas d'ombre. |
Carte plane de l'Egypte ancienne. Le soleil n'est pas à la verticale, les obélisques d'Alexandrie et de Syène projettent des d'ombres de longueurs égales. |
Carte de l'Egypte ancienne (projection). Le soleil peut se trouver à la verticale de Syène mais pas d'Alexandrie., l'obélisque de Syène ne projette aucune ombre contrairement à celui d'Alexandrie. |
Ératosthène ne trouva qu'une seule réponse possible à cette question: il fallait que la surface de la Terre fût courbe. Et plus cette courbure serait marquée, plus la différence entre les longueurs des ombres serait grande. Le Soleil est Si loin de nous que, lorsqu'ils atteignent la Terre, ses rayons sont parallèles. C'est donc l'angle qu'ils forment avec un objet qui détermine la longueur de l'ombre que celui-ci va projeter. D'après la différence observée entre la longueur des ombres, Alexandrie devait se trouver approximativement à sept degrés de Syène; ce qui veut dire que, Si l'on prolonge des piquets verticaux plantés en ces deux endroits jusqu'au centre de la Terre, ils formeront en se coupant un angle de sept degrés. Sept degrés représentent à peu près le cinquième de trois cent soixante degrés, mesure de la circonférence totale de la Terre. Eratosthène savait qu'il y avait près de huit cents kilomètres entre Alexandrie et Syène, car il avait engagé un homme pour parcourir cette distance et la mesurer. Cinquante fois huit cents kilomètres font quarante mille kilomètres: telle devait être la circonférence de la Terre. Cette réponse était la bonne. Avec pour seuls instruments quelques bouts de bois, ses yeux, ses jambes, son intelligence et son goût de l'expérience, Eratosthène mesura la circonférence de la Terre avec un pourcentage d'erreur très faible. Ce résultat est d'autant plus extraordinaire que cela se passait il y a deux mille deux cents ans. Eratosthène est donc le premier homme qui ait essayé de mesurer la taille d'une planète, et qui y soit arrivé.
Les navigateurs méditerranéens étaient alors réputés, et Alexandrie certainement le plus grand port du monde. Sachant que la Terre était une sphère de modeste diamètre, comment ne pas être tenté par de nouvelles explorations, par la découverte de terres inconnues, et, pourquoi pas, le tour du monde? Quatre siècles plus tôt, une flotte phénicienne au service du pharaon égyptien Néchao avait fait le tour de l'Afrique. Partis de la mer Rouge, probablement sur de frêles esquifs découverts, les marins avaient longé la côte Est de l'Afrique pour rejoindre l'Atlantique et remonter ensuite jusqu'à la Méditerranée. Ce voyage épique avait duré trois ans, à peu près le temps qu'il faut à un vaisseau spatial comme Voyager pour aller de la Terre à Saturne. A la suite de la découverte d'Eratosthène, de longs voyages maritimes furent entrepris par des navigateurs aventureux et courageux. Leurs navires étaient minuscules, leurs instruments rudimentaires. Ils avançaient à l'estime et suivaient la côte le plus longtemps possible.
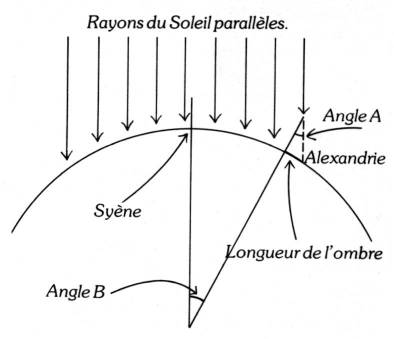
On peut mesurer l'angle A à partir de la longueur de l'ombre relevée à Alexandrie. la géométrie la plus élémentaire nous apprend que l'angle B est égal à l'angle a. ainsi, en mesurant la longueur de l'ombre relevée à Alexandrie, Erasthène en déduisit que Syène était éloignée d'Alexandrie par un arc de 7° (A=B=7°) sur la circonférence de la terre.
D'après Carl Sagan (Cosmos)
|
angle |
7° |
360° |
|
arc de cercle |
5000 stades |
257000 stades |
257.000 x 157 = 40349000 m, soit 40349 km.
(cliquez sur le lien ci-dessus)